Different Weights

About falling bodies Galileo*, years ago, tells how two mobiles with different “weight” but equal density move with equal speed, trying in this way to disprove an Aristotle’s statement…

“mobiles of the same material and different weight, when moved through the same medium, receive velocities proportional to their weights“

Galileo’s disproof is based on a very simple reasoning… not very appropriate to discredit Aristotle, father of the Logic… and on the ambiguity of the term “weight”… indeed this disproof comes from a radical change of scenario, since Galileo takes approximately the example of apples, now smaller now bigger, falling vertically in his garden…

Aristotle’s mobile is instead a celestial body moved by his Prime Mover, moving in his Universe of concentric Spheres and describing a Perfect Motion… what’s more, for Aristotle cause of the movement is always a force…

So, for celestial bodies, “weights” are the forces acting on them, originated by a Prime Mover and directed towards Eutòpia*, “velocities” are the ones received by the rotation of the concentric Spheres, causes of the movement.

Observation and Logic lead Aristotle to say that, for mobiles in circular motion, the rotational speeds of their concentric Spheres are proportional to the forces pushing them towards Eutòpia, in such a way that the mobiles are always in a condition of equilibrium… rotations constantly preventing the mobiles to fall on Eutòpia.

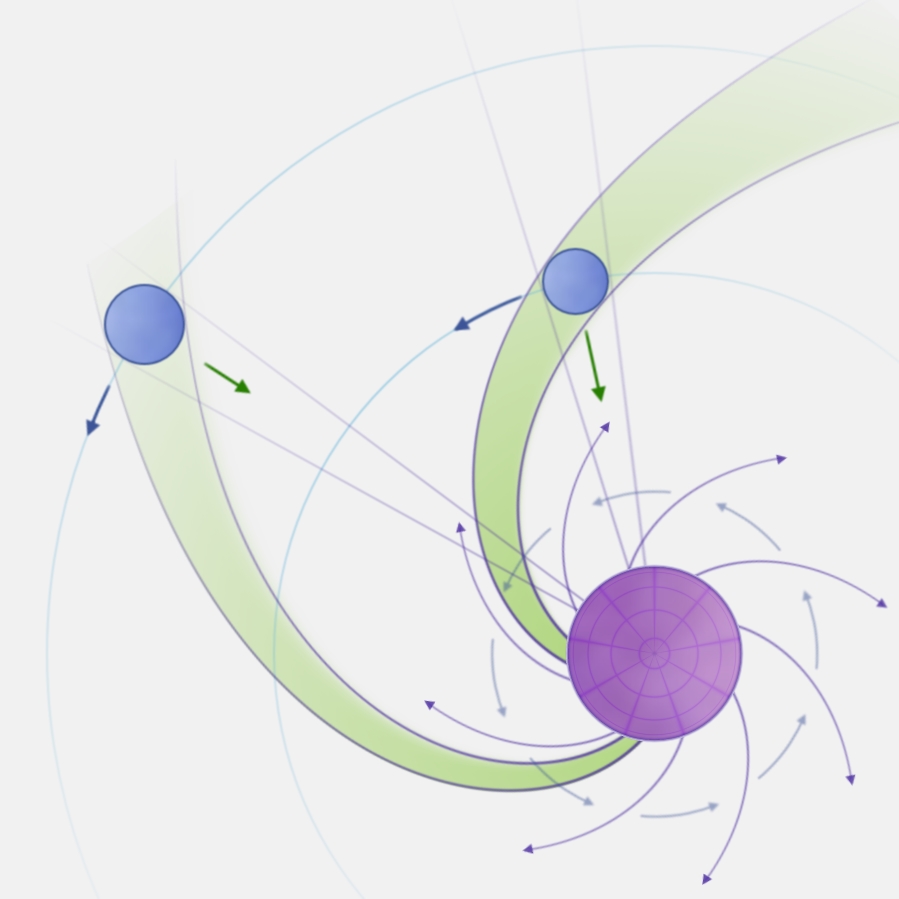
Let’s consider a Satellite revolving around a Planet…

• its momentum depends on its matter
• the gravitational force acting on it depends on the power of its Center of force

Let’s suppose, now, to have, on the same orbit (at the same speed), a Satellite with double amount of matter and double volume, considering that, for a sphere, doubling the radius is more than doubling the surface, which is more than doubling the volume…

• its momentum would be double
• the power of its Center of force would be most likely less than double

consequently the gravitational force wouldn’t be able to bend adequately the trajectory of the “double Satellite”… i.e. the old orbit would be no longer appropriate to the new Inertia of the Satellite… then, necessarily, the “double Satellite” will go to occupy a more external orbit, on which it will find again an equilibrium ratio between “velocity” and “weight”.

So bigger Moons, with equal density, occupy slower orbits on which they are “lighter”.

 

*******
Eutòpia ⇒ Planet Earth and Aristotle’s Center of the Universe Galileo ⇒ Galileo Galilei