The Dance of Epimetheus and Janus

Epimetheus and Janus are two Satellites of Saturn that chase each other.

Each Satellite, individually taken, would move in Perfect Motion…

the revolutions of the two satellites, which share approximately the same orbit, are instead affected by a mutual interaction that implies a variation on the Spin and gravitational forces acting on the Satellites.

The problem, dealt in an Aristotelian way, has a simple solution:
the Spin determines the orbital speed of the satellites… and (in a Perfect Motion) the ratio between speed and gravity of satellites is a constant depending on the Planet.

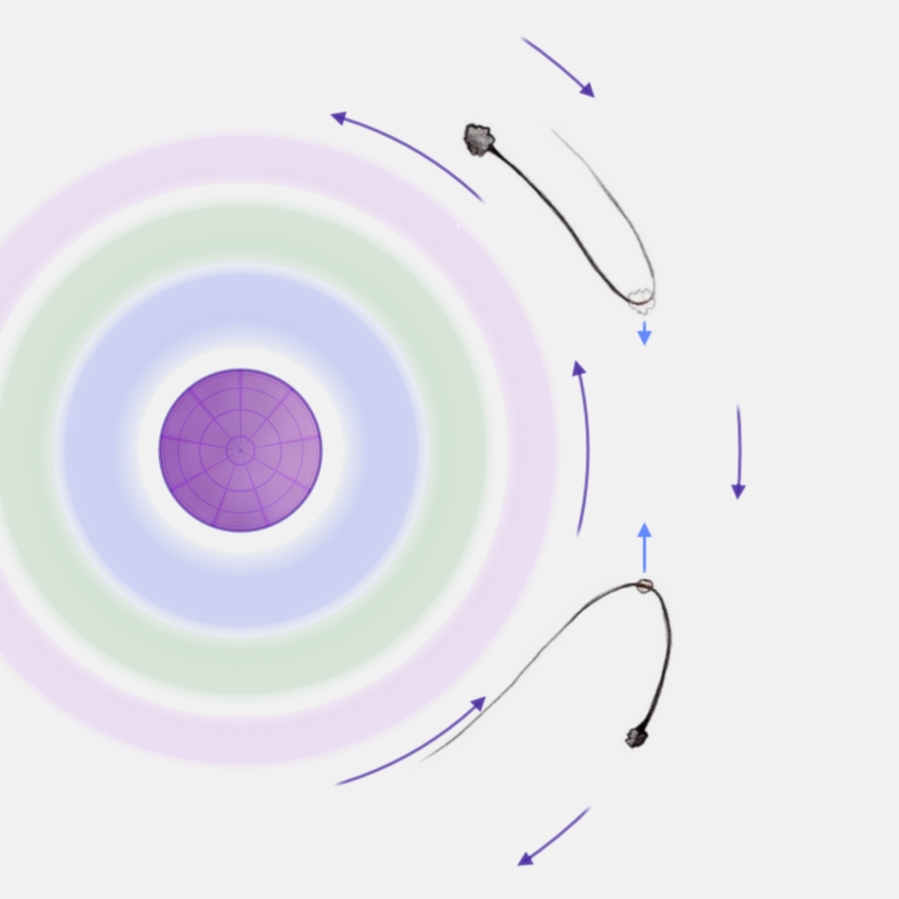
Then, considering (to simplify) just the variation on the Spin acting on the Satellites, in the phase of proximity

• the Spin force acting on the “Satellite that precedes” decreases… then the gravity works more on the Satellite, pushing it towards a more internal and faster orbit (a fall)
• the Spin force acting on the “Satellite that follows” increases… then the gravity works less on the Satellite, that gradually shifts towards a more external and slower orbit (an escape)
  

After the phase of proximity, when the mutual interaction between the Satellites disappears, they find themselves in two orbits not exactly of their competence, then the “Satellite that preceded” begins slowly to open its orbit, the “Satellite that followed” to close it… and then they meet again with alternate roles.

The exchange of the orbits (as well as the tadpole orbits for trojan asteroids) is a stable phenomenon… two Satellites could share, in case, the same orbit, but they should never interact with each other… just a precarious equilibrium, not likely in Solaris*.

 

*******
Solaris ⇒ Solar System